Caratteristiche e tipi del triangolo angolare acuto

il triangoli triangoli sono quelli i cui tre angoli interni sono angoli acuti; cioè, la misurazione di ciascuno di questi angoli è inferiore a 90 gradi. Non avendo un angolo retto, abbiamo che il teorema di Pitagora non è soddisfatto per questa figura geometrica.

Pertanto, se vogliamo avere qualche tipo di informazione su uno qualsiasi dei suoi lati o angoli, è necessario utilizzare altri teoremi che ci permettono di avere accesso a tali dati. Quelli che possiamo usare sono il teorema del seno e il teorema del coseno.

indice

• 1 caratteristiche
  • 1.1 Teorema del seno
  • 1.2 Teorema del coseno
• 2 tipi
  • 2.1 Triangoli triangolari equilateri
  • 2.2 Triangoli acuti isosceli
  • 2.3 Scala triangoli acután
• 3 Risoluzione dei triangoli acuti
  • 3.1 Esempio 1
  • 3.2 Esempio 2
• 4 riferimenti

lineamenti

Tra le caratteristiche di questa figura geometrica possiamo evidenziare quelle che sono date dal semplice fatto di essere un triangolo. Tra questi dobbiamo:

- Un triangolo è un poligono che ha tre lati e tre angoli.

- La somma dei suoi tre angoli interni è uguale a 180 °.

- La somma di due dei suoi lati è sempre maggiore della terza.

Ad esempio, vediamo il seguente triangolo ABC. In generale, identifichiamo i loro lati con lettere minuscole e i loro angoli con lettere maiuscole, in modo che un lato e l'angolo opposto abbiano la stessa lettera.

Per le caratteristiche già fornite, sappiamo che:

A + B + C = 180 °

a + b> c, a + c> b e b + c> a

La caratteristica principale che distingue questo tipo di triangolo dal resto è che, come già accennato, i suoi angoli interni sono acuti; cioè, la misura di ciascuno dei suoi angoli è inferiore a 90 °.

I triangoli acutángulos, insieme ai triangoli obtusángulos (quelli in cui uno dei suoi angoli ha una misura maggiore di 90 °), fanno parte del set di triangoli obliqui. Questo set è composto da triangoli che non sono rettangoli.

Quando si formano triangoli obliqui, dobbiamo usare il teorema del seno e il teorema del coseno per risolvere problemi che coinvolgono triangoli acuti.

Teorema di Sine

Il teorema del seno afferma che il rapporto tra un lato e il seno del suo angolo opposto è uguale al doppio del raggio del cerchio formato dai tre vertici di quel triangolo. Quello è:

2r = a / sin (A) = b / sin (B) = c / sin (C)

Teorema del coseno

D'altra parte, il teorema del coseno ci fornisce queste tre uguaglianze per ogni triangolo ABC:

a²= b² + c² -2bc * cos (A)

B²= a² + c² -2ac * cos (B)

c²= a² + b² -2ab * cos (C)

Questi teoremi sono anche noti come la legge del seno e della legge del coseno, rispettivamente.

Un'altra caratteristica che possiamo dare dei triangoli è che due di questi sono uguali se soddisfano uno dei seguenti criteri:

- Se hanno tutti e tre i lati uguali.

- Se hanno un lato e due angoli uguali tra loro.

- Se hanno due lati e un angolo uguale.

tipo

Possiamo classificarli con triangoli basati sui loro lati. Questi possono essere:

Triangoli triangolari equilateri

Sono i triangoli acutángulos che hanno tutti i loro lati uguali e, quindi, tutti i loro angoli interni hanno lo stesso valore, che è A = B = C = 60 gradi.

Ad esempio prendiamo il triangolo seguente, i cui lati a, bec hanno un valore di 4.

Triangoli acuti isosceli

Questi triangoli, oltre ad avere angoli interni acuti, hanno la caratteristica di avere due dei loro lati uguali e il terzo, che è generalmente preso come base, diverso.

Un esempio di questo tipo di triangoli può essere uno la cui base è 3 e gli altri due lati hanno un valore di 5. Con queste misure avremmo gli angoli opposti ai lati uguali con il valore di 72,55 ° e l'angolo opposto di la base sarebbe 34,9 °.

Scala triangoli acutángulos

Questi sono i triangoli che hanno tutti i loro lati diversi da due a due. Pertanto, tutti i suoi angoli, oltre a essere inferiori a 90 °, sono diversi due a due.

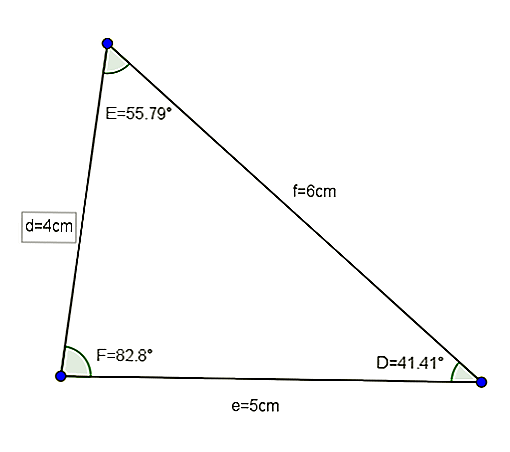
Il triangolo DEF (le cui misure sono d = 4, e = 5 e f = 6 e i suoi angoli sono D = 41,41 °, E = 55,79 ° e F = 82,8 °) è un buon esempio di triangolo acuto scalene.

Risoluzione dei triangoli acuti

Come abbiamo detto in precedenza, per la soluzione di problemi che coinvolgono triangoli acuti, è necessario l'uso dei teoremi del seno e del coseno.

Esempio 1

Dato un triangolo ABC con angoli A = 30 °, B = 70 ° e lato a = 5 cm, vogliamo conoscere il valore dell'angolo C e i lati be c.

La prima cosa che facciamo è usare il fatto che la somma degli angoli interni di un triangolo è 180 °, in modo da ottenere il valore dell'angolo C.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Cancelliamo C e ce ne siamo andati:

C = 180 ° - 100 ° = 80 °

Come già conosciamo i tre angoli e un lato, possiamo usare il teorema del seno per determinare il valore dei lati rimanenti. Per il teorema dobbiamo:

a / sin (A) = b / sin (B) e a / sin (A) = c / (sin (C)

Cancelliamo b dall'equazione e dobbiamo:

b = (a * sin (B)) / sin (A) ≈ (5 * 0.940) / (0.5) ≈ 9.4

Ora abbiamo solo bisogno di calcolare il valore di c. Procediamo analogamente come nel caso precedente:

c = (a * sin (C)) / sin (A) ≈ (5 * 0.984) / (0.5) ≈ 9.84

In questo modo otteniamo tutti i dati del triangolo. Come possiamo vedere, questo triangolo rientra nella categoria del triangolo acuto scaleno.

Esempio 2

Dato un triangolo DEF con lati d = 4 cm, e = 5 cm e f = 6 cm, vogliamo conoscere il valore degli angoli di detto triangolo.

In questo caso useremo la legge del coseno, che ci dice che:

d²= e² + f² - 2efcos (D)

Da questa equazione possiamo cancellare cos (D), che ci dà come risultato:

Cos (D) = ((4)² - (5)² -(6)²)/(-2*5*6) =0.75

Da qui abbiamo quel D≈ 41.41 °

Ora usando il teorema di senom abbiamo la seguente equazione:

d / (sin (D) = e / (sin (E)

Eliminando il peccato (E), dobbiamo:

sin (E) = e * sin (D) / d = (5 * 0.66) / 4 ≈ 0.827

Da qui abbiamo che E≈55.79 °

Infine, usando che la somma degli angoli interni di un triangolo è 180 °, abbiamo F≈82,8 °.

riferimenti

1. Landaverde, F. d. (1997). Geometria (ristampa ed.). Progress.
2. Leake, D. (2006). Triangoli (illustrati a cura di). Heinemann-Raintree.
3. Leal G. Juan Manuel. (2003). Geometria geometrica plana.CODEPRE
4. Ruiz, Á., & Barrantes, H. (2006). Geometrie. Tecnologia CR
5. Sullivan, M. (1997). Trigonometria e geometria analitica. Pearson Education.