Matematica discreta Cosa servono, teoria degli insiemi

il matematica discreta corrisponde a un'area della matematica che è responsabile dello studio dell'insieme dei numeri naturali; cioè, l'insieme di numeri numerabili e infiniti numerabili in cui gli elementi possono essere contati separatamente, uno per uno.

Questi set sono noti come set discreti; Un esempio di questi insiemi sono numeri interi, grafici o espressioni logiche e sono applicati in diversi campi della scienza, principalmente in informatica o informatica.

indice

• 1 Descrizione
• 2 Qual è l'uso della matematica discreta?
  • 2.1 Combinatorio
  • 2.2 Teoria della distribuzione discreta
  • 2.3 Teoria dell'informazione
  • 2.4 Calcolo
  • 2.5 Crittografia
  • 2.6 Logica
  • 2.7 Teoria dei grafici
  • 2.8 Algebra
  • 2.9 Geometria
• 3 Teoria dei set
  • 3.1 Set finito
  • 3.2 Set di conti infiniti
• 4 Discretizzazione
• 5 riferimenti

descrizione

In discreti processi matematici sono numerabili, basati su numeri interi. Ciò significa che i numeri decimali non vengono utilizzati e, pertanto, l'approssimazione oi limiti non vengono utilizzati, come in altre aree. Ad esempio, uno sconosciuto può essere uguale a 5 o 6, ma mai 4.99 o 5.9.

D'altra parte, nella rappresentazione grafica le variabili saranno discrete e sono date da un insieme finito di punti, che sono contati uno per uno, come visto nell'immagine:

La matematica discreta nasce dalla necessità di ottenere uno studio esatto che può essere combinato e testato, per applicarlo in diverse aree.

Qual è l'uso della matematica discreta?

La matematica discreta è utilizzata in più aree. Tra i principali ci sono i seguenti:

combinatoria

Studia gli insiemi finiti in cui gli elementi possono essere ordinati o combinati e contati.

Teoria della distribuzione discreta

Studiare eventi che si verificano in spazi in cui i campioni possono essere numerabili, in cui vengono utilizzate distribuzioni continue per approssimare distribuzioni discrete o in modo opposto.

Teoria dell'informazione

Si riferisce alla codifica delle informazioni, utilizzate per la progettazione, la trasmissione e la memorizzazione dei dati, come ad esempio i segnali analogici.

informatica

Attraverso la matematica discreta i problemi vengono risolti utilizzando algoritmi, oltre a studiare ciò che può essere calcolato e il tempo necessario per farlo (complessità).

L'importanza della matematica discreta in quest'area è aumentata negli ultimi decenni, specialmente per lo sviluppo dei linguaggi di programmazione e software.

crittografia

Si basa su una matematica discreta per creare strutture di sicurezza o metodi di crittografia. Un esempio di questa applicazione sono le password, che inviano separatamente bit che contengono informazioni.

Attraverso lo studio, le proprietà degli interi e dei numeri primi (teoria dei numeri) possono creare o distruggere questi metodi di sicurezza.

logica

Vengono usate strutture discrete, che di solito formano un insieme finito, per dimostrare teoremi o, per esempio, verificare il software.

Teoria dei grafi

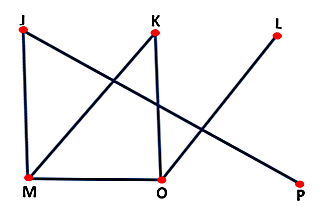
Permette la risoluzione di problemi logici, usando nodi e linee che formano un tipo di grafico, come mostrato nell'immagine seguente:

algebra

È un'area strettamente legata alla matematica discreta perché le espressioni algebriche sono discrete. Attraverso questo, vengono sviluppati circuiti elettronici, processori, programmazione (algebra booleana) e database (algebra relazionale).

geometria

Studia le proprietà combinatorie di oggetti geometrici, come il rivestimento del piano. D'altra parte, la geometria computazionale consente di sviluppare problemi geometrici applicando algoritmi.

Teoria dei set

Negli insiemi di matematica discreti (numerabili e infiniti numerabili) sono l'obiettivo principale di studio. La teoria degli insiemi è stata pubblicata da George Cantor, che ha dimostrato che tutti i set infiniti hanno le stesse dimensioni.

Un insieme è un raggruppamento di elementi (numeri, cose, animali e persone, tra gli altri) che sono ben definiti; cioè, esiste una relazione in base alla quale ogni elemento appartiene a un insieme e viene espresso, ad esempio, a ∈ A.

In matematica ci sono diversi set che raggruppano determinati numeri in base alle loro caratteristiche. Quindi, ad esempio, hai:

- Set di numeri naturali N = {0, 1, 2, 3, 4, 5, 6, ... + ∞}.

- Set di interi E = {-∞ ..., -3, -2, -1, 0, 1, 2, 3, ... + ∞}.

- Sottoinsieme di numeri razionali Q * = {-∞ ..., - ¼, - ½, 0, ¼, ½, ... ∞}.

- Set di numeri reali R = {-∞ ..., - ½, -1, 0, ½, 1, ... ∞}.

I set sono denominati con lettere dell'alfabeto, in lettere maiuscole; mentre gli elementi sono denominati in lettere minuscole, all'interno di parentesi graffe ({}) e separati da virgole (,). Di solito sono rappresentati in diagrammi come quelli di Venn e di Caroll, oltre che a livello computazionale.

Con operazioni di base come unione, intersezione, complemento, differenza e prodotto cartesiano, gli insiemi ei loro elementi sono gestiti, in base alla relazione di appartenenza.

Esistono diversi tipi di set, i più studiati nella matematica discreta sono i seguenti:

Set finito

È uno che ha un numero finito di elementi e corrisponde a un numero naturale. Quindi, per esempio, A = {1, 2, 3,4} è un insieme finito che ha 4 elementi.

Set di conti infinito

È quello in cui c'è una corrispondenza tra gli elementi di un insieme e i numeri naturali; vale a dire che da un elemento tutti gli elementi di un insieme possono essere elencati successivamente.

In questo modo, ogni elemento corrisponderà a ciascun elemento dell'insieme di numeri naturali. Ad esempio:

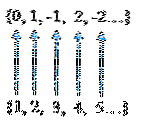
L'insieme di interi Z = {... -2, -1, 0, 1, 2 ...} può essere elencato come Z = {0, 1, -1, 2, -2 ...}. In questo modo è possibile fare una corrispondenza uno-a-uno tra gli elementi di Z e i numeri naturali, come mostrato nell'immagine seguente:

discretizzazione

È un metodo utilizzato per risolvere i problemi (modelli ed equazioni) continui ad essere convertiti in problemi discreti, in cui è nota la soluzione per approssimare la soluzione del problema costante.

In altre parole, la discretizzazione cerca di estrarre una quantità finita da un insieme infinito di punti; in questo modo, un'unità continua viene trasformata in unità individuali.

Generalmente questo metodo viene utilizzato nell'analisi numerica, come per esempio nella soluzione di un'equazione differenziale, per mezzo di una funzione che è rappresentata da una quantità finita di dati nel suo dominio, anche quando è continua.

Un altro esempio di discretizzazione è il suo uso per convertire un segnale analogico in digitale, quando unità di segnale continue vengono convertite in singole unità (sono discretizzate) e quindi codificate e quantizzate per ottenere il segnale digitale.

riferimenti

1. Grimaldi, R. P. (1997). Matematica discreta e combinatoria. Addison Wesley Iberoamericana.
2. Ferrando, V. Gregori. (1995). Matematica discreta Reverte.
3. Jech, T. (2011). Imposta la teoria. Stanford Encyclopedia of Philosophy.
4. José Francisco Villalpando Becerra, A. G. (2014). Matematica discreta: applicazioni ed esercizi. Grupo Editorial Patria.
5. Landau, R. (2005). Computing, A First Course in Scientific.
6. Merayo, F. G. (2005). Matematica discreta. Thomson Editorial.
7. Rosen, K. H. (2003). Matematica discreta e sue applicazioni. McGraw-Hill.
8. Schneider, D. G. (1995). Un approccio logico alla matematica discreta.